Find Parametric Equation of a Line | Solution & Examples | Query Point Official
Find Parametric Equation of a Line | Step-by-Step Solution
Find a parametric equation of the line through `\bar u ` and `\bar v` , where
Given that
let suppose that
Now, we find the direction vector
Here
`a = 6, b = - 7` c = 11
Now parametric equations are
`x = x_0 + at`
`\Rightarrow x = - 6 + 6t`
`y = y_0 + bt`
`\Rightarrow y = 3 - 7t`
`z = z_0 + ct`
`\Rightarrow z = - 4 + 11t`
Related Posts
Frequently Asked Questions (FAQs)
What is the parametric equation of a line?
The parametric equation of a line represents each coordinate of the line as a function of a parameter, usually denoted by t.
Why do we use parametric equations?
Parametric equations are useful because they describe lines in both two-dimensional and three-dimensional space and work even for vertical lines.
What information is required to find a parametric equation of a line?
To find a parametric equation, we need a point on the line and a direction vector.
Is parametric form important for exams?
Yes, parametric equations of lines are commonly asked in university-level Mathematics, Engineering Mathematics, and Vector Analysis exams.
What parameter is usually used?
The parameter t is commonly used, but any variable can be chosen as a parameter.
Explore more about LINEAR ALGEBRA in Mathematics Notes & MCQs.
Query Point Official – Smart Notes for Exams & Conceptual Learning

.png)



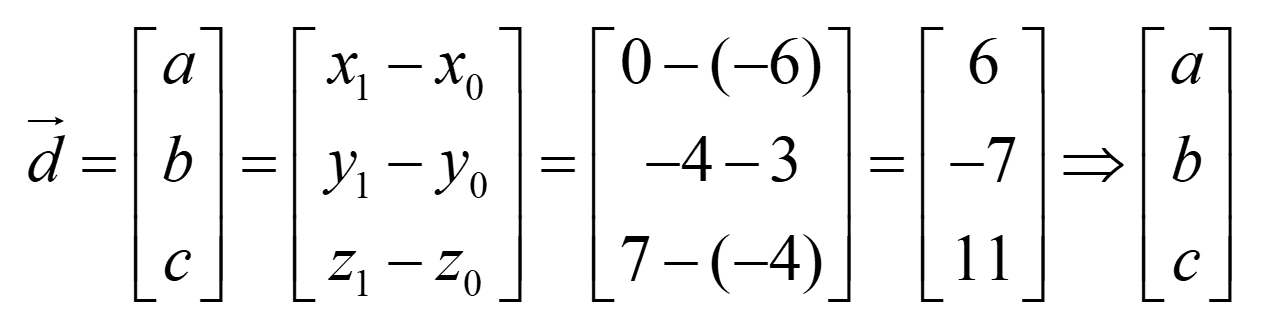
No comments