Determine Values of h and k for System of Linear Equations | QueryPoint Official
Determine Values of h and k for a System of Linear Equations
.png)
Determine the value(s) of h and k such that the given system
`x + 5y - 4z = 3,`
`3x + 12y - 12z = - 3,`
`2x + 7y + hz = k`
has
1. no solution,
2.
a unique solution,
3. many
solutions.
Answer:
Given system
`x + 5y - 4z = 3`
`3x + 12y - 12z = - 3`
`2x + 7y + hz = k`
Now, in the matrix form
let
So,
`AX = B`
Now, in the form of Augmented matric
As
`C = [A:B]`
Now, their consistent matrices are
Now, discuss the given conditions:
i. NO SOLUTION
`If h = - 8 and k \ne - 6`
then `the\[R(A) < R(B)`, there will be no solution.
For that R(A)=2 and R(B)=3.
ii. UNIQUE SOLUTION
`If h \ne - 8 and k \ne - 6`
then the R(A) = R(B) = 3 = no. of unknown, there will be unique solutions.
For that R(A)=3 and R(B)=3.
iii. MANY SOLUTION
If `h = - 8 and k = - 6`
then the R(A) = R(B) = 2 < no. of unknown, there will be many solutions.
Like that R(A)=2 and R(B)=2.
Related Topics
- Find Out Index Numbers (Algebra Concepts)
- Laws of Logic – Verify Statements
- Truth Table Determination (Boolean Logic)
Frequently Asked Questions (FAQs)
1. What does it mean for lines to be perpendicular?
Two lines are perpendicular if they intersect at a right angle (90°). In coordinate geometry, this occurs when the slopes multiply to −1.
2. How do you find slope from an equation?
For a line in the form \(Ax + By + C = 0\), the slope is \(-\frac{A}{B}\).
3. Can lines with zero slope be perpendicular?
Yes. A line with zero slope (horizontal) is perpendicular to a line with undefined slope (vertical).
Explore more about LINEAR ALGEBRA in Mathematics Notes & MCQs.
Query Point Official – Smart Notes for Exams & Conceptual Learning
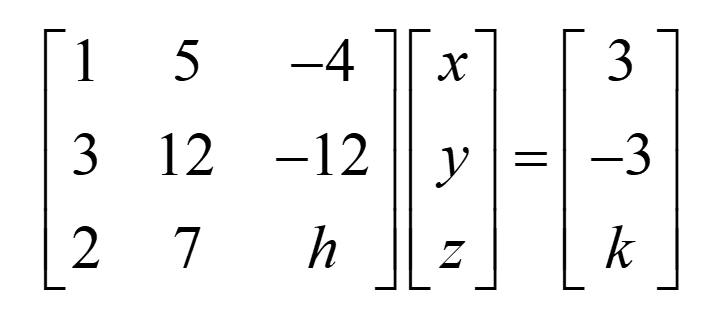
No comments